線型系
\[
\frac{\mathrm{d}\mathbf{u}}{\mathrm{d}t} = \mathbf{Au}
\]
を考える。 ここで \(\mathbf{u}(t)\) は時刻 \(t\) での状態、 \(\mathbf{A}\) は線型化された力学演算子である。
この演算子が \[
\mathbf{A} = \begin{bmatrix}-1 & \cot\theta \\ 0 & -2\end{bmatrix}
\]
で与えられているときの時間発展 \(\mathrm{d}\mathbf{u}/\mathrm{d}t\) を矢印で描き、大きさ \(1\) の摂動を円で、 \((\mathbf{A} + \mathbf{A}^\dagger)/2\) の最大固有値に対応する単位固有ベクトル(数値的固有値の最大実部)と最も縮小する固有ベクトルを破線で描く。 順を追って示す。
Base Rには円を函数はないので、区分的に直線を描く。
plot(NULL, xlim = c(-1, 1), ylim = c(-1, 1), asp = 1,
main = "Circle", xlab = "X", ylab = "Y",
cex.main = 1.5, cex.lab = 1.5, cex.axis = 1.5)
angle <- pi * seq(0, 2 * pi, length.out = 361)
lines(cos(angle), sin(angle), col = "black", lwd = 2)
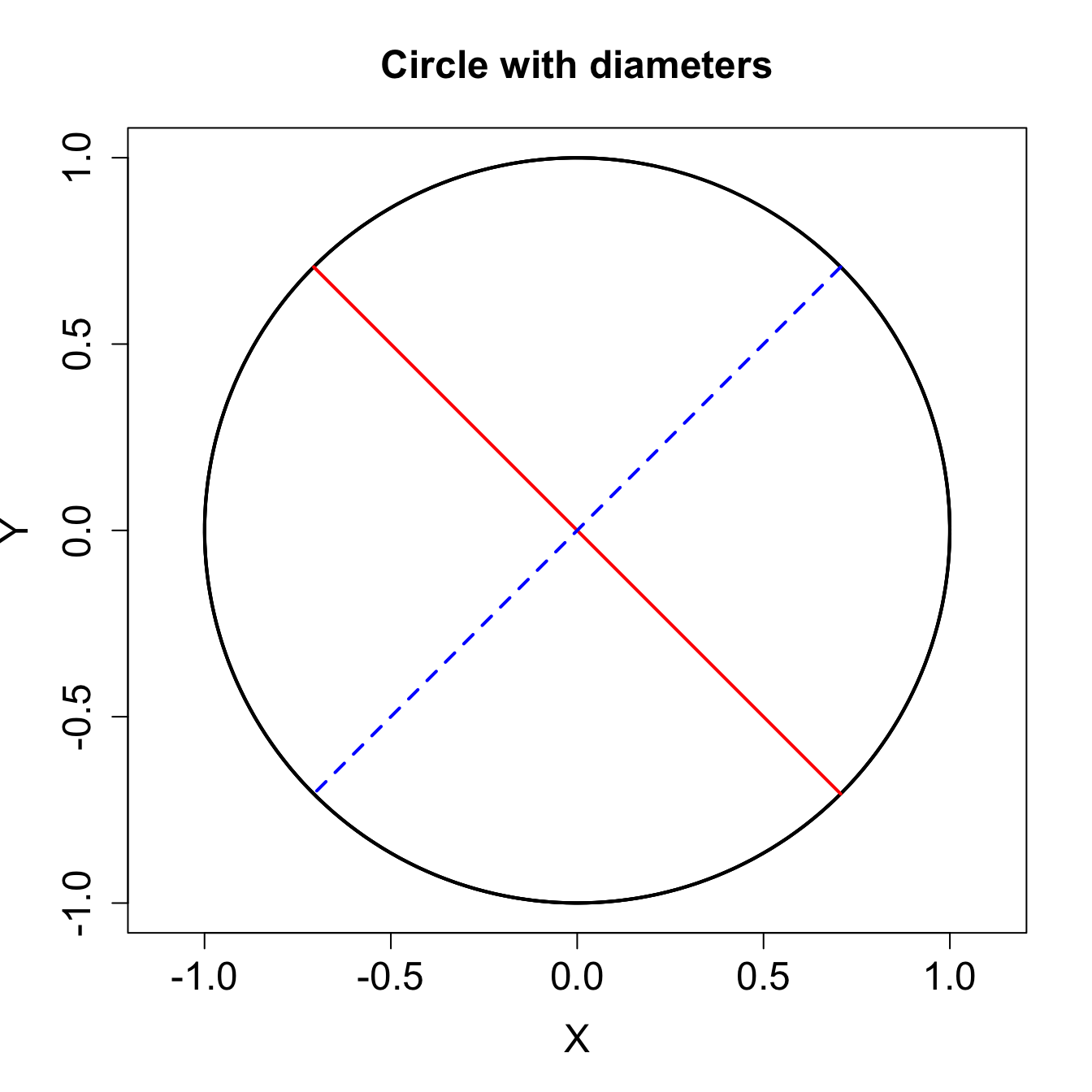
最大瞬時成長率を持つ単位ノルム摂動は、 \((\mathbf{A} + \mathbf{A}^\dagger) / 2\) を固有値解析することにより得られ、 対応する固有ベクトルは \(x\) 軸と \(\alpha = \arctan(\sin\theta - 1) / \cos\theta\) の角をなす。 これと直交する方向が最も縮小する。 \(\theta\rightarrow 0\) の極限では \(\alpha = -\pi / 4\) である。 abline() は簡単に直線を描くことができるが、範囲を区切ることはできないので、 segments() で始点と終点を指定して描画する。
plot(NULL, xlim = c(-1, 1), ylim = c(-1, 1), asp = 1,
main = "Circle with diameters", xlab = "X", ylab = "Y",
cex.main = 1.5, cex.lab = 1.5, cex.axis = 1.5)
angle <- pi * seq(0, 2 * pi, length.out = 361)
lines(cos(angle), sin(angle), col = "black", lwd = 2)
segments(cos(3 * pi/4), sin(3 * pi/4), cos(-pi/4), sin(-pi/4), col = "red", lwd = 2)
segments(cos(pi/4), sin(pi/4), cos(5 * pi/4), sin(5 * pi/4), col = "blue", lwd = 2, lty = 2)
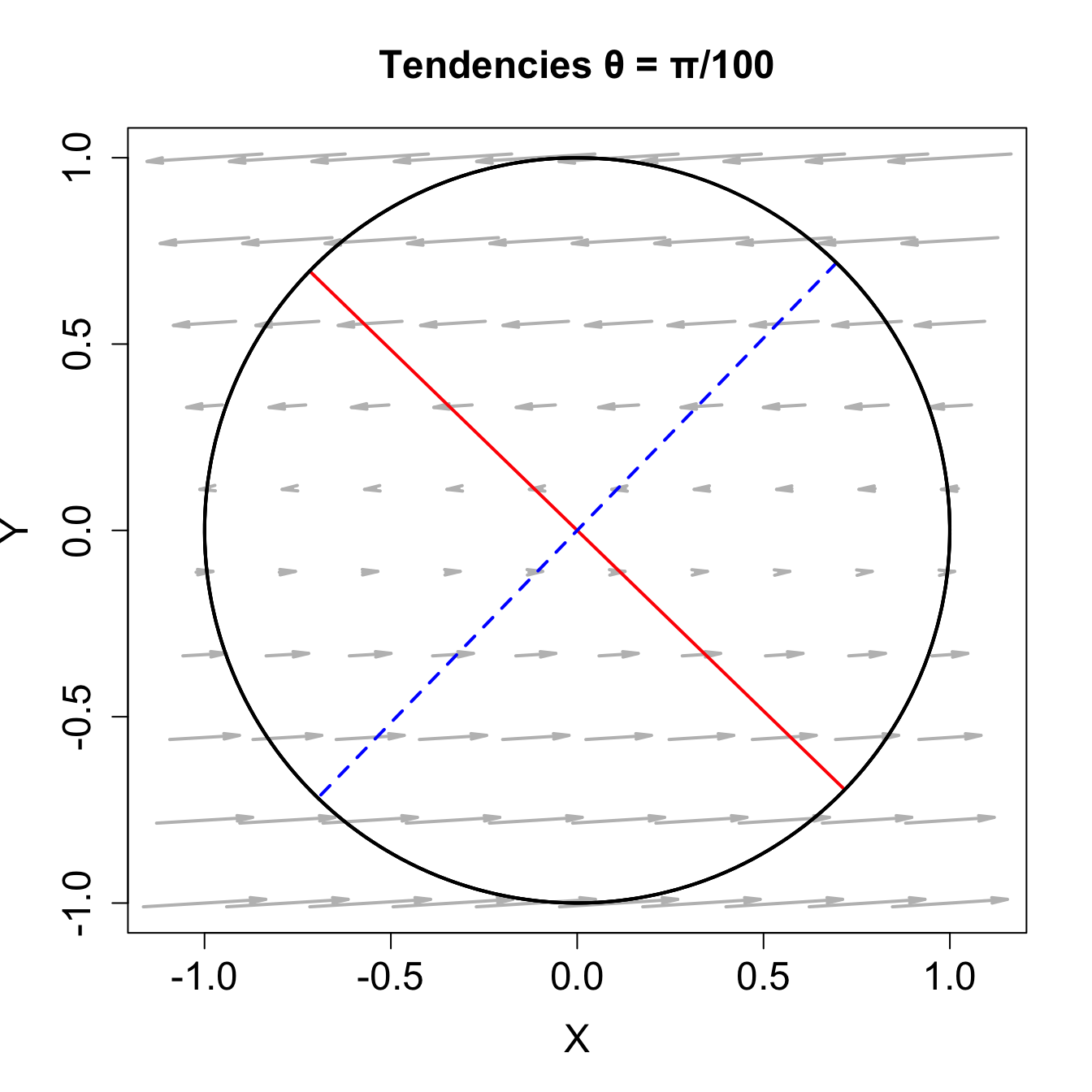
\(\theta = \pi / 100\) の場合ついて、 \(\mathrm{d}\mathbf{A}/\mathrm{d}t\) を矢印で描く。 矢印を描くには、 arrows() を使う。 segments() 同様 arrows() も始点と終点を指定する。 Rでは、スカラーは要素が1のベクトルなので、一つの矢印を描くのも、たくさん描くのも同様にできる。 矢印の中心を格子点の中心に置くことにする。 終点と始点は、適切な拡大縮小率を掛けて \(x,\,y\) 方向の成分を座標にそれぞれ加減する。 座標の位置は、expand.grid() を使って \(x,\,y\) 方向それぞれ一次元のベクトルから生成する。
x <- seq(-1, 1, length.out = 10)
y <- seq(-1, 1, length.out = 10)
theta <- pi / 100
alpha <- atan((sin(theta) - 1) / cos(theta))
cot <- function(theta) {
cos(theta) / sin(theta)
}
amat <- matrix(c(-1, 0, -cot(theta), -2), nrow = 2)
xy <- expand.grid(x = x, y = y)
X <- xy$x
Y <- xy$y
uv <- amat %*% t(as.matrix(xy))
a <- 0.005
u <- a * uv[1, ]
v <- a * uv[2, ]
plot(NULL, xlim = c(-1, 1), ylim = c(-1, 1), asp = 1,
main = "Tendencies θ = π/100", xlab = "X", ylab = "Y",
cex.main = 1.5, cex.lab = 1.5, cex.axis = 1.5)
arrows(X - u, Y - v, X + u, Y + v,
col = "gray", lwd = 2, length = 0.1, angle = 10)
segments(cos(alpha), sin(alpha), cos(alpha + pi), sin(alpha + pi), col = "red", lwd = 2)
segments(cos(alpha + pi/2), sin(alpha + pi/2), cos(alpha + 3*pi/2), sin(alpha + 3*pi/2), col = "blue", lwd = 2, lty = 2)
angle <- pi * seq(0, 2 * pi, length.out = 361)
lines(cos(angle), sin(angle), col = "black", lwd = 2)