Lanczos法

numerics
package
大規模行列に対する固有値分解
Author

榎本剛

Published

July 31, 2025

Lanczos法は、大規模行列に対する固有値・固有ベクトルを計算するために用いられる。 特に、系の自由度よりも少ない数の固有値・固有ベクトルを求める場合に有用である。

数値天気予報のアンサンブル摂動や感度解析に応用されている (Buizza et al. 1993)。

SVD via Lanczos Iterationを参考にLanczos法について概要を述べ、Rで実装し、 svd() と比較する。

Krylov部分空間

\(\mathbf{A}\) を \(n\times n\) の正方行列、\(1 \le k \le n\) とすると、Krylov（クリロフ）部分空間は

\[ \mathcal{K}_k = \text{span}\{\mathbf{x}, \mathbf{Ax}, \mathbf{A}^2\mathbf{x},\dots,\mathbf{A}^{k-1}\mathbf{x}\} \] と表される。 Lanczos法は、行列をこの部分空間に投影することにより、固有値・固有ベクトルの近似解を求める。 すなわち、共軛勾配法と同様に Krylov部分空間法の一つである。

Lanczos反復

\(n\times n\) 行列 \(\mathbf{A}\) を三重対角化する。

\[ \mathbf{T}_k = \mathbf{Q}_k^\dagger\mathbf{A}\mathbf{Q}_k \]

ここで、 _k$ は\(\boldsymbol\alpha = [\alpha_1,\,\alpha_2,\,\dots,\,\alpha_k]\)を対角成分、 \(\boldsymbol\beta = [\beta_1,\,\beta_2,\,\dots,\,\beta_k]\) 副対角成分とする \(k \times k\) の $ 三重対角行列、 \(\mathbf{Q}_k = [\mathbf{q}_1, \mathbf{q}_2, \dots, \mathbf{q}_k]\) は列ベクトル \(\mathbf{q}_i\) を並べた \(n\times k\) 行列である。

まず、\(\mathbf{q}_0 = 0\)とし、\(\mathbf{q}_1\)を乱数で初期化する。

\(j = 1,\,2\,\dots,k\) に対して、以下のLanczos反復を行う。

  1. \(\mathbf{v} = \mathbf{A}\mathbf{q}_i\)
  2. \(\alpha_i = \mathbf{q}_i^\mathrm{T}\mathbf{v}\)
  3. \(\mathbf{v} = \mathbf{v} - \beta_{i-1}\mathbf{q}_{i-1} - \alpha_i\mathbf{q}_i\)
  4. \(\beta_i = \|\mathbf{v}\|_2\)
  5. \(\mathbf{q}_{i+1} = \mathbf{v} / \beta_i\)

\(\mathbf{H}\) を明示的に作ることを避け、 \(\mathbf{A}(q_{m+1}, \dots q_{m+n})^\mathrm{T}\) と \(\mathbf{A}^\mathrm{T}(q_{1}, \dots q_{n})\) を計算している。

Code 
l2norm <- function(x) sqrt(sum(x * x))

lanczos <- function(amat, k = 1, calc.norm = l2norm) {
  m <- nrow(amat)
  n <- ncol(amat)
  
  alpha <- numeric(k)
  beta <- numeric(k - 1)
  
  q <-matrix(0, m + n, k)
  q[, 1] <- runif(m + n)
  q[, 1] <- q[, 1] / calc.norm(q[, 1])
  v <- c(amat %*% q[(m+1):(m+n), 1], t(amat) %*% q[1:m, 1])
  alpha[1] <- crossprod(q[, 1], v)
  v <- v - alpha[1] * q[, 1]
  for (i in 2:k) {
    beta[i - 1] <- calc.norm(v)
    q[, i] <- v / beta[i - 1]
    v <- c(amat %*% q[(m+1):(m+n), i], t(amat) %*% q[1:m, i])
    alpha[i] <- crossprod(q[, i], v)
    v <- v - beta[i - 1] * q[, i - 1] - alpha[i] * q[, i]
  }
  list(alpha = alpha, beta = beta, q = q)
}

特異値分解

三重対角行列 \(\mathbf{T}_k\) を固有値分解することにより、固有値と固有ベクトル \(\mathbf{S}_k\) を得る。 \(\mathbf{T}_k\) の固有値は\(\mathbf{A}\) の固有値の近似であり、 \(\mathbf{A}\) の固有ベクトルは \(\mathbf{Q}_k\mathbf{S}_k\) で近似される。

\(m\times n\) の行列 \(\mathbf{A}\) の特異値分解は、\(\mathbf{A}^\dagger\mathbf{A}\) の固有値分解から求めることができる。

右特異ベクトルも同時に求めるには、\((m+n)\times (m+n)\) 行列

\[ \mathbf{H} = \begin{bmatrix} \mathbf{0}_{m \times m} & \mathbf{A}\\ \mathbf{A}^\dagger & \mathbf{0}_{n \times n} \end{bmatrix} \]

の固有値分解を行えばよい。 \(\mathbf{Y}_k = \sqrt{2}\mathbf{Q}_k\mathbf{S}_k\) の最初の \(m\) 行が左特異ベクトル、残り \(n\) 行が転置されていない右特異ベクトルを表す。

Code 
tridiagonal <- function(alpha, beta) {
  n <- length(alpha)
  td <- diag(alpha)
  for (i in 1:(n - 1)) {
    td[i, i + 1] <- beta[i]
    td[i + 1, i] <- beta[i]
  }
  td
}

lanczos_svd <- function(amat, k, calc.norm = l2norm) {
  m <- nrow(amat)
  n <- ncol(amat)
  if (m < n) stop("m < n")

  nc <- min(m + n, k)
  k2 <- 2 * k
  
  lz <- lanczos(amat, k = k2)
  tmat <- tridiagonal(lz$alpha, lz$beta)
  ev <- eigen(tmat, symmetric = TRUE)
  d <- ev$values[1:nc]
  uv <- sqrt(2) * (lz$q %*% ev$vectors)
  u <- uv[1:m, 1:nc]
  v <- uv[(m + 1):(m + n), 1:nc]
  list(d = d, u = u, v = v)
}

実行例

\(300 \times 50\) の行列に対する特異値分解を行い、svd() と比較する。

Code 
set.seed(514)
m <- 300
n <- 50
x <- matrix(rnorm(m * n), m, n)
k <- 20
firstfew <- 1:4
lz <- lanczos_svd(x, k = k)
sv <- svd(x)
df <- data.frame(
  method = rep(c("lz", "sv"), k),
  uv = c(rep("u", 2 * k), rep("v", 2 * k)),
  mode = as.vector(rbind(1:k, 1:k)),
  d = as.vector(rbind(lz$d, sv$d[1:k]))
)
vec <- matrix(0, 4 * k, length(firstfew))
for (i in 1:k) {
  vec[2 * (i - 1) + 1, ] <- lz$u[firstfew, i]
  vec[2 * (i - 1) + 2, ] <- sv$u[firstfew, i]
  vec[2 * (k + i - 1) + 1, ] <- lz$v[firstfew, i]
  vec[2 * (k + i - 1) + 2, ] <- sv$v[firstfew, i]
}
df <- cbind(df, vec)
head(df)
  method uv mode        d           1            2            3           4
1     lz  u    1 24.13591 -0.05354460  0.109305205 -0.002478789 -0.05285225
2     sv  u    1 24.13591 -0.05354596  0.109304061 -0.002478183 -0.05285274
3     lz  u    2 23.62877  0.05266008 -0.028730425  0.046056005 -0.05855043
4     sv  u    2 23.62877  0.05262743 -0.028758545  0.046070908 -0.05856183
5     lz  u    3 22.73793 -0.13940413  0.011378436  0.063098084 -0.10492187
6     sv  u    3 22.73812 -0.14145087  0.009369697  0.064082735 -0.10535872

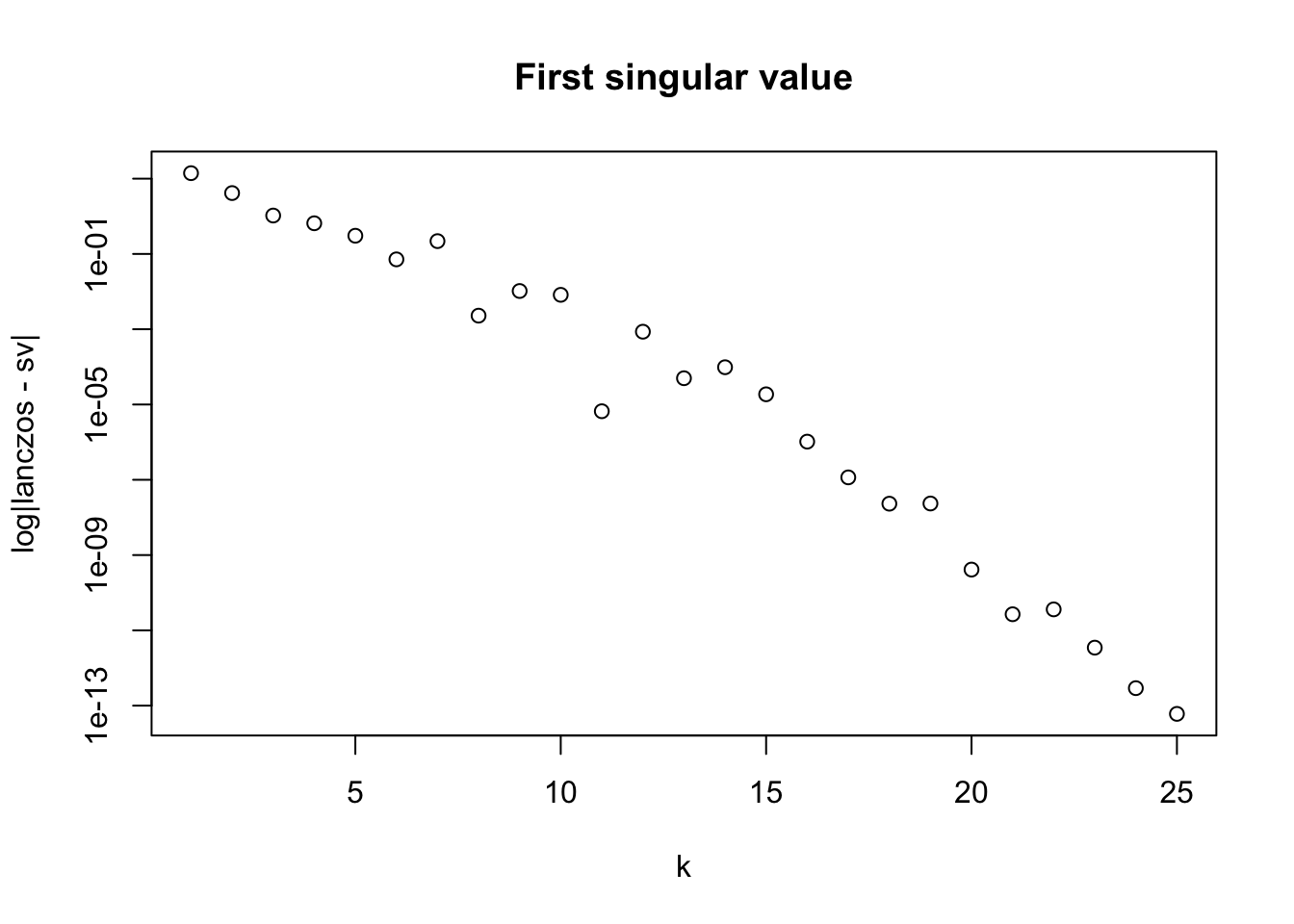
最大特異値の反復回数\(k\) に対する依存性を調べてみる。

set.seed(514)
d <- numeric(n)
for (k in 1:n) {
  lz <- lanczos_svd(x, k = k)
  d[k] <- lz$d[1]
}
plot(1:(n/2), abs(d[1:(n/2)] - sv$d[1]), log = "y",
     xlab = "k", ylab = "log|lanczos - sv|",
     main = "First singular value")

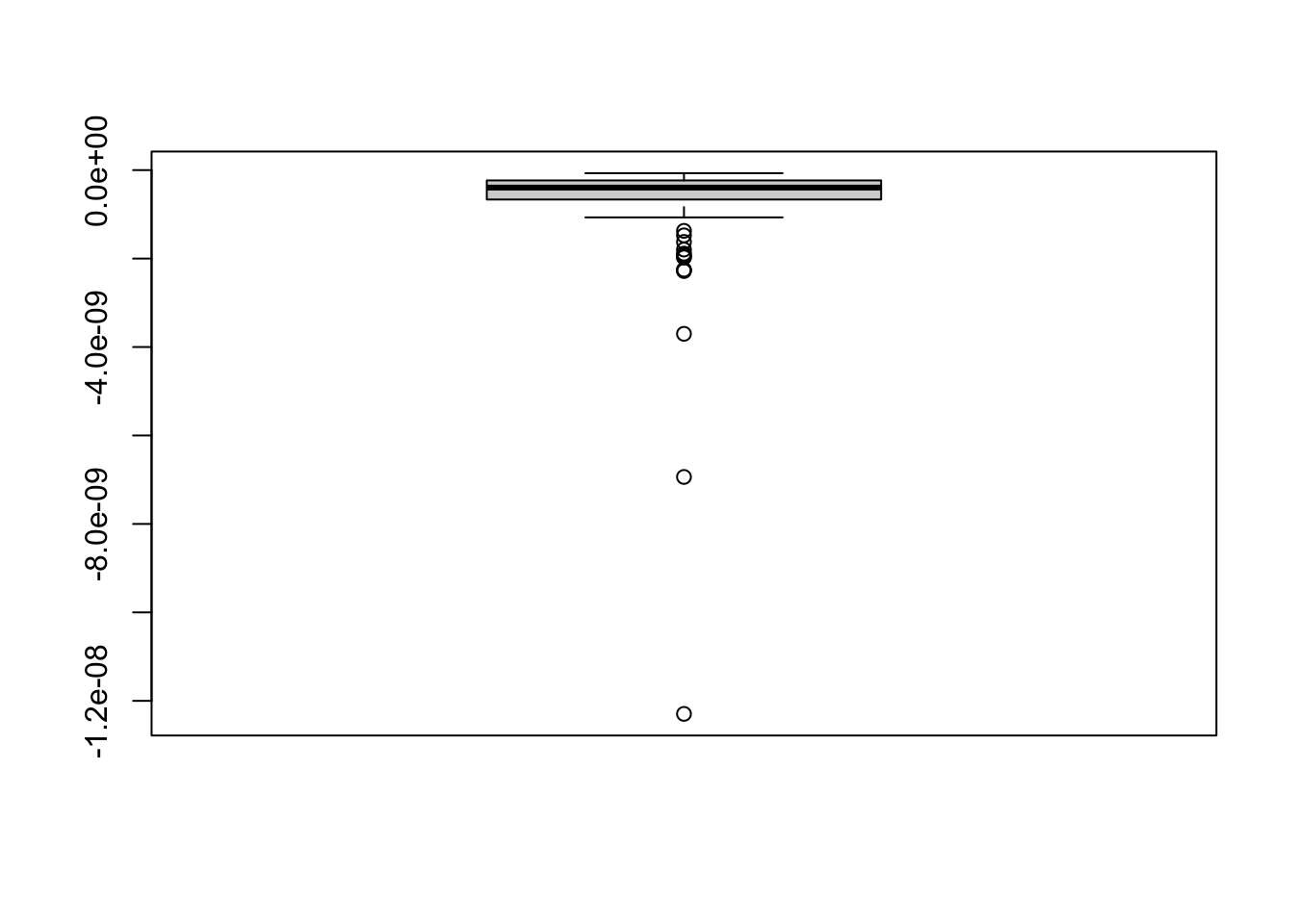
乱数に対する依存性を調べる。

set.seed(514)
nd <- 100
k <- 20
d <- numeric(nd)
for (i in 1:nd) {
  lz <- lanczos_svd(x, k = k)
  d[i] <- lz$d[1]
}
boxplot(d - sv$d[1])

乱数の影響は誤差程度であり、少なくとも第一モードに関しては気にしなくてよさそうだ。

パッケージ

大規模な固有値問題にはFortran 77で書かれた ARPACK が使われてきた （後継は arpack-ng）。 C++で実装し直された SpectrA には、Rのインターフェースがあり、疎行列や行行列ベクトル積を計算する函数に対応している。

References

Buizza, R., J. Tribbia, F. Molteni, and T. Palmer, 1993: Computation of optimal unstable structures for a numerical weather prediction model. Tellus, 45A, 388–407, https://doi.org/10.1034/j.1600-0870.1993.t01-4-00005.x.